MIT researchers develop methods to control transformer sensitivity with proven Lipschitz boundaries and MUON
Training large transformers to stabilize In deep learning, it has been a long-term challenge, especially as the size and expressiveness of the model grows. MIT researchers address an ongoing problem: Instable activation Loss spikes caused by unrestricted weight and activation specifications. Their solution is to execute Proofable Lipschitz boundary On the transformer * Adjust weights by spectrum – * No need to use activation normalization, QK Norm or Logit soft patch tips.
What is Lipschitz’s binding? Why execute it?
one Lipschitz binding On a neural network, the quantized output can vary the maximum amount in response to the perturbation of input (or weight). Mathematically speaking, the function ffff is kkk-lipschitz, if: ∥f(x1)-f(x2)∥≤k∥x1-x2∥x1,x2 | f(x_1) – f(x_2)|leq k | x_1 – x_2 | forall x_1,x_2∥f(x1)-f(x2)∥≤k∥x1 -x2∥x1,x2
- Under Lipschitz combines greater robustness and predictability.
- Crucial for stability, robustness, privacy, and generalization, with lower limits, which means the network is less sensitive to change or adversarial noise.
Motive and problem statement
Traditionally, training stable transformer scale involves Various “Band-Aids” Stability Tips:
- Layer normalization
- QK normalization
- logit tanh softc
However, these do not directly address the basic spectral specification (maximum singular) growth of weights, which is the root cause of explosive activation and training instability, especially in large models.
this Central hypothesis: If we spectically adjust the weight itself (just an optimizer or activation), we can maintain strict control over Lipschitzness and may resolve instability at its source.
Key innovation
Weight spectroscopy and sub-optimizer
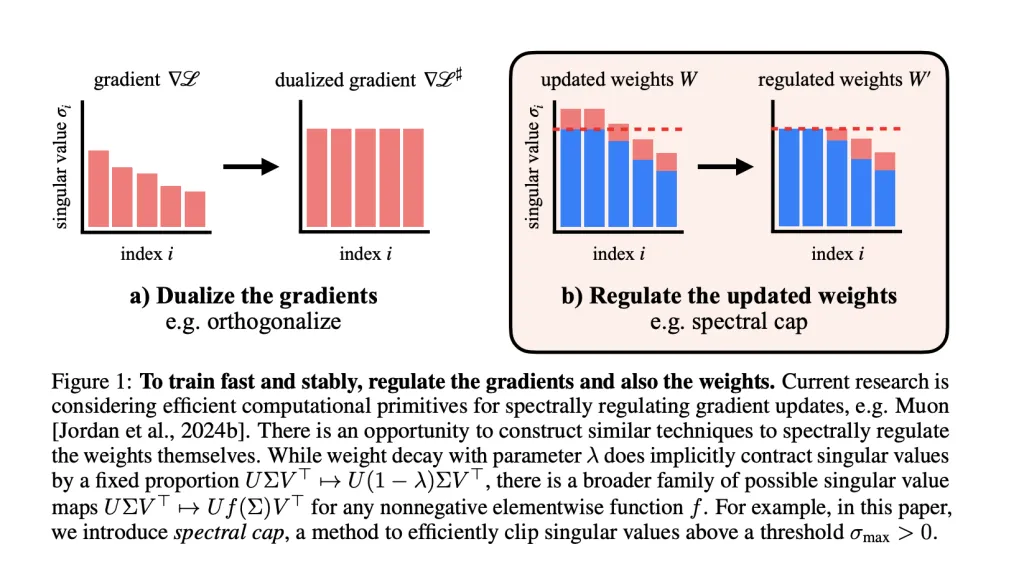
- mom Optimizer spectral regularization gradientensuring that each gradient step does not add spectral standards beyond the set limits.
- Researchers Extend adjustment to weight: After each step, they apply the operation to Limit singular values Each weight matrix. The activation specification remains very small As a result, the values compatible with FP8 accuracy in their GPT-2 gauge transformers are rarely exceeded.
Eliminate stability techniques
In all experiments, There is no layer normalization, no QK specification, no logit tanh is used. However,
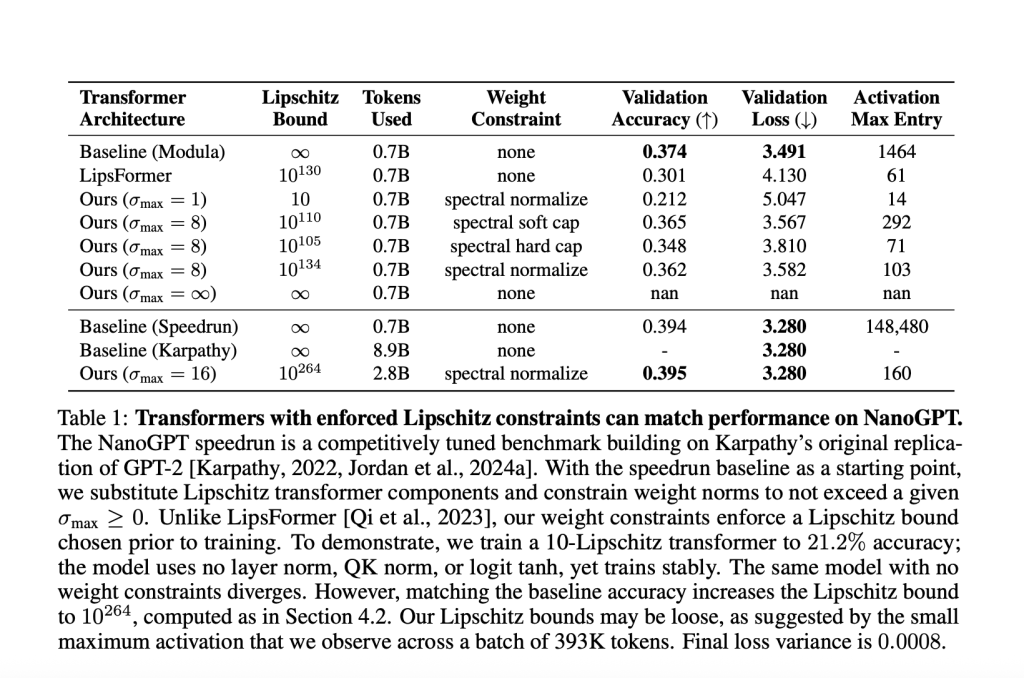
- Maximum activation entry Their GPT-2 scale transformers never exceed ~100, And the unconstrained baseline exceeds 148,000.
Table sample (Nanoput experiment)
| Model | Maximum activation | Layer stability techniques | Verification accuracy | Lipschitz binding |
|---|---|---|---|---|
| Baseline (Speedrun) | 148,480 | Yes | 39.4% | ∞ |
| Lipschitz transformer | 160 | Nothing | 39.5% | 10⁰²⁶⁴ |
Methods to implement Lipschitz constraints
All kinds of Weight specification constraint method They were explored and compared:
- Maintain high performance,,,,,
- Ensure Lipschitz bindingand
- Optimized Performance – Lupuchit tradeoff.

technology
- Weight attenuation: Standard method, but not always strictly spectroscopic specification.
- Spectral normalization: Ensure the highest value is capped, but may affect all odd values around the world.
- Spectral soft cap: The novel method smoothly and effectively applies σ→min(σmax,σ)sigma to all singular values in the minimum value (sigma_{text{max}},sigma)σ→min(σmax,σ) in parallel (approximate using singular units). This was designed for Muon’s high-stable updates to achieve tight boundaries.
- Spectral hammer: Set the maximum singular value to σmaxSigma_{text {max}}σmax, which is best for ADAMW Optimizer.
Experimental results and insights
Model evaluation of various sizes
- Shakespeare (small transformer,
- With the following proven Lipschitz combination, 60% verification accuracy can be achieved.
- In validation losses, poor performance over baseline.
- Nanogpt (145 million parameters):
- Bind with Lipschitz
- arrive match Strong baseline (accuracy is 39.4%), Requires a large upper limit of 1026410^{264} 10264. This underscores the strict constraints of Lipschitz often trade in a expressive manner on a large scale.
Weight constraint method efficiency
- MUON + Spectral Cap: Leadership trade-offs– Lower Lipschitz constants are used for matching or better validation losses compared to ADAMW+weight decay.
- Spectral soft cap and normalization (Under Muon) Always achieve the best boundaries in terms of loss-Lipschitz tradeoffs.
Stability and robustness
- Adversarial robustness Increases dramatically on the lower Lipschitz boundaries.
- In experiments, the accuracy of models with constrained Lipschitz constants decreased a lot under adversarial attacks compared to unconstrained baselines.
Activation range
- Adjust the spectral weight: Maximum activation is still small (near FP8 compatible) compared to the unbounded baseline, even on a large scale.
- This opens up the path Low-precision training and reasoning In hardware, smaller activations reduce computing, memory, and power costs.
Restrictions and opening issues
- Choose the “tightest” tradeoff For weight specifications, logit scaling and attention scaling still depends on the scan, not the principle.
- The current upper limit is loose: The calculated global boundaries may be astronomy-large (e.g. 1026410^{264} 10264), while the actual activation specification is still small.
- It is not clear whether the baseline performance of strict Lipschitz boundary matching can be used as the scale increases –More research is needed.
in conclusion
Spectral weight adjustment (especially paired with the MUON optimizer) can stably train large transformers with forced Lipschitz boundaries without activating normalization or other band-aid tricks. This solves deeper instability and keeps activations within a compact, predictable range, greatly improving adversarial robustness and potential hardware efficiency.
This work line points to a new, effective computing foundation for neural network regulation and has extensive applications in privacy, security and low-precision AI deployment.
Check Paper, github pages and hug facial project pages. Check out ours anytime Tutorials, codes and notebooks for github pages. Also, please stay tuned for us twitter And don’t forget to join us 100K+ ml reddit And subscribe Our newsletter.
Sana Hassan, a consulting intern at Marktechpost and a dual-degree student at IIT Madras, is passionate about applying technology and AI to address real-world challenges. He is very interested in solving practical problems, and he brings a new perspective to the intersection of AI and real-life solutions.



