Focal Loss and Binary Cross-Entropy: A Practical Guide to Imbalanced Classification

Binary Cross Entropy (BCE) is the default loss function for binary classification, but it fails severely on imbalanced data sets. The reasons are subtle but important: BCE measures the errors of both classes equallyeven if a certain type is extremely rare.

Imagine two predictions: the minority class sample with true label 1 is predicted to be 0.3, and the majority class sample with true label 0 is predicted to be 0.7. Both produce the same BCE value: −log(0.3). But should these two errors be treated equally? In an imbalanced data set, absolutely not – errors on a small number of samples are much more costly.

this is exactly where focus loss It reduces the contribution of simple, confident predictions and amplifies the impact of difficult, minority examples. The model therefore focuses less on overwhelmingly simple groups and more on the patterns that really matter. Check The complete code is here.

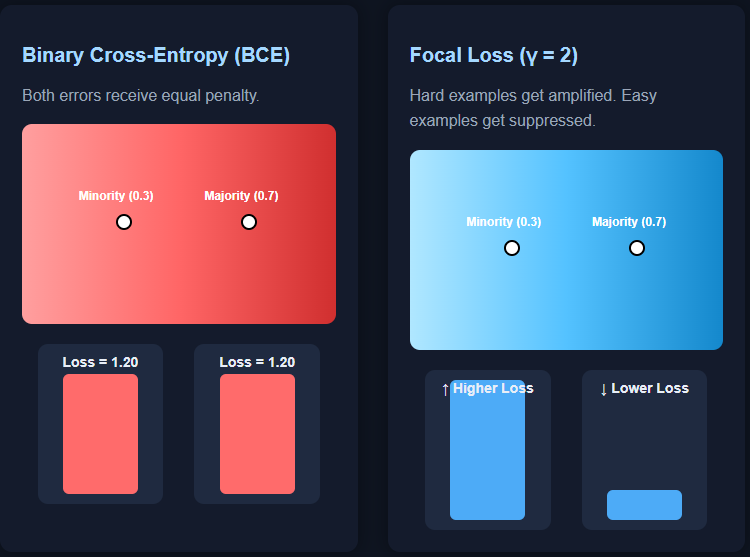
In this tutorial, we demonstrate this effect by training two identical neural networks (one using BCE and the other using focal loss) on a dataset with an imbalance ratio of 99:1 and comparing their behavior, decision regions and confusion matrices. Check The complete code is here.

Install dependencies

pip install numpy pandas matplotlib scikit-learn torch

Create an imbalanced data set

We create a comprehensive binary classification dataset 99:1 unbalanced vs. 6000 Sample using make_classification. This ensures that almost all samples belong to the majority class, making it an ideal setting to demonstrate why BCE gets into trouble and how Focal Loss works. Check The complete code is here.

import numpy as np
import matplotlib.pyplot as plt
from sklearn.datasets import make_classification
from sklearn.model_selection import train_test_split
import torch
import torch.nn as nn
import torch.optim as optim

# Generate imbalanced dataset
X, y = make_classification(
    n_samples=6000,
    n_features=2,
    n_redundant=0,
    n_clusters_per_class=1,
    weights=[0.99, 0.01],   
    class_sep=1.5,
    random_state=42
)

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.3, random_state=42
)

X_train = torch.tensor(X_train, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32).unsqueeze(1)
X_test  = torch.tensor(X_test,  dtype=torch.float32)
y_test  = torch.tensor(y_test,  dtype=torch.float32).unsqueeze(1)

Create a neural network

We define a simple neural network with two hidden layers to keep the experiment lightweight and focused on the loss function. This small architecture is sufficient to learn decision boundaries in 2D datasets while clearly highlighting the difference between BCE and focal loss. Check The complete code is here.

class SimpleNN(nn.Module):
    def __init__(self):
        super().__init__()
        self.layers = nn.Sequential(
            nn.Linear(2, 16),
            nn.ReLU(),
            nn.Linear(16, 8),
            nn.ReLU(),
            nn.Linear(8, 1),
            nn.Sigmoid()
        )
    def forward(self, x):
        return self.layers(x)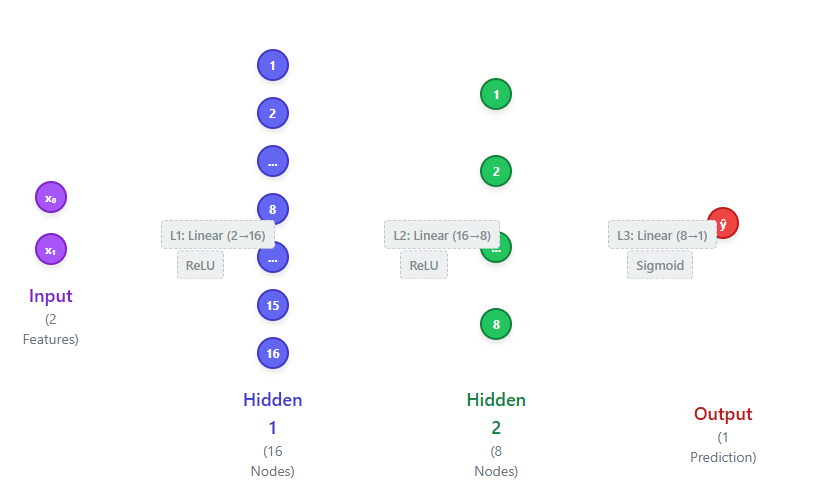

focus loss implementation

This class implements a focal loss function that modifies binary cross-entropy by downweighting simple examples and focusing training on difficult misclassified examples. The gamma term controls how much simple samples are suppressed, while the alpha assigns higher weight to minority classes. Together they help the model learn better on imbalanced data sets. Check The complete code is here.

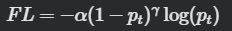
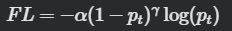
class FocalLoss(nn.Module):
    def __init__(self, alpha=0.25, gamma=2):
        super().__init__()
        self.alpha = alpha
        self.gamma = gamma

    def forward(self, preds, targets):
        eps = 1e-7
        preds = torch.clamp(preds, eps, 1 - eps)
        
        pt = torch.where(targets == 1, preds, 1 - preds)
        loss = -self.alpha * (1 - pt) ** self.gamma * torch.log(pt)
        return loss.mean()

Training model

We define a simple training loop, optimize the model using the chosen loss function and evaluate the accuracy on the test set. We then train two identical neural networks – one with the standard BCE loss and the other with the focal loss – allowing us to directly compare the performance of each loss function on the same imbalanced dataset. The accuracy of printing highlights the performance gap between BCE and Focal Loss.

Although BCE shows very high accuracy (98%), this is misleading because the dataset is severely imbalanced – predicting almost everything as most classes still yields high accuracy. Focal Loss, on the other hand, improves minority class detection, which is why its slightly higher accuracy (99%) is more meaningful in this case. Check The complete code is here.

def train(model, loss_fn, lr=0.01, epochs=30):
    opt = optim.Adam(model.parameters(), lr=lr)

    for _ in range(epochs):
        preds = model(X_train)
        loss = loss_fn(preds, y_train)
        opt.zero_grad()
        loss.backward()
        opt.step()

    with torch.no_grad():
        test_preds = model(X_test)
        test_acc = ((test_preds > 0.5).float() == y_test).float().mean().item()
    return test_acc, test_preds.squeeze().detach().numpy()

# Models
model_bce = SimpleNN()
model_focal = SimpleNN()

acc_bce, preds_bce = train(model_bce, nn.BCELoss())
acc_focal, preds_focal = train(model_focal, FocalLoss(alpha=0.25, gamma=2))

print("Test Accuracy (BCE):", acc_bce)
print("Test Accuracy (Focal Loss):", acc_focal)

Draw decision boundaries

The BCE model produces an almost flat decision boundary, predicting only the majority class and completely ignoring minority samples. This happens because, in imbalanced datasets, BCE is dominated by majority class examples and learns to classify almost everything into that class. In contrast, the Focal Loss model shows more refined and meaningful decision boundaries, successfully identifies more minority areas and captures patterns that BCE cannot learn. Check The complete code is here.

def plot_decision_boundary(model, title):
    # Create a grid
    x_min, x_max = X[:,0].min()-1, X[:,0].max()+1
    y_min, y_max = X[:,1].min()-1, X[:,1].max()+1
    xx, yy = np.meshgrid(
        np.linspace(x_min, x_max, 300),
        np.linspace(y_min, y_max, 300)
    )
    grid = torch.tensor(np.c_[xx.ravel(), yy.ravel()], dtype=torch.float32)
    with torch.no_grad():
        Z = model(grid).reshape(xx.shape)

    # Plot
    plt.contourf(xx, yy, Z, levels=[0,0.5,1], alpha=0.4)
    plt.scatter(X[:,0], X[:,1], c=y, cmap='coolwarm', s=10)
    plt.title(title)
    plt.show()

plot_decision_boundary(model_bce, "Decision Boundary -- BCE Loss")
plot_decision_boundary(model_focal, "Decision Boundary -- Focal Loss")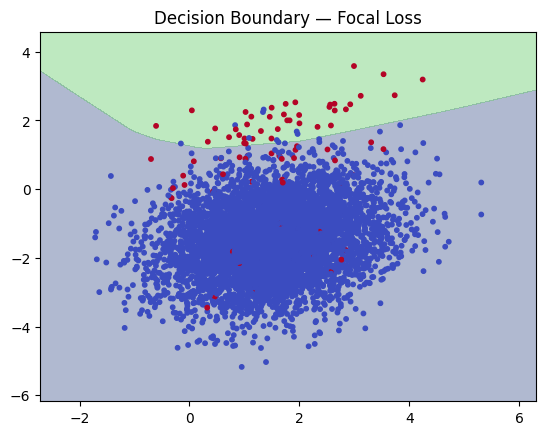

Plot confusion matrix

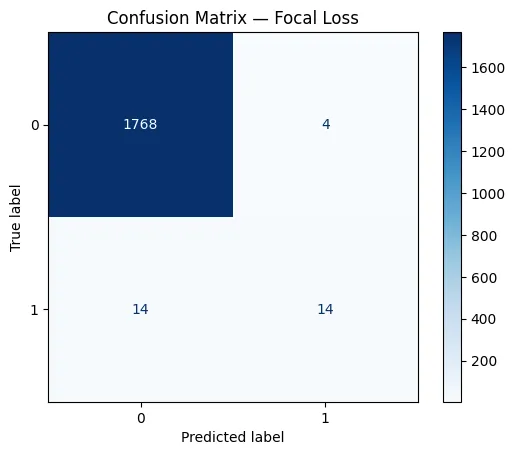
In the confusion matrix of the BCE model, the network correctly identified only 1 minority class sample and misclassified 27 of them as the majority class. This shows that BCE cannot predict almost everything as the majority class due to imbalance. In comparison, the Focal Loss model correctly predicted 14 minority samples and reduced misclassifications from 27 to 14. This shows how focal loss places more emphasis on difficult minority class examples, enabling the model to learn decision boundaries that actually capture the rare class rather than ignoring it. Check The complete code is here.

from sklearn.metrics import confusion_matrix, ConfusionMatrixDisplay

def plot_conf_matrix(y_true, y_pred, title):
    cm = confusion_matrix(y_true, y_pred)
    disp = ConfusionMatrixDisplay(confusion_matrix=cm)
    disp.plot(cmap="Blues", values_format="d")
    plt.title(title)
    plt.show()

# Convert torch tensors to numpy
y_test_np = y_test.numpy().astype(int)

preds_bce_label   = (preds_bce > 0.5).astype(int)
preds_focal_label = (preds_focal > 0.5).astype(int)

plot_conf_matrix(y_test_np, preds_bce_label, "Confusion Matrix -- BCE Loss")
plot_conf_matrix(y_test_np, preds_focal_label, "Confusion Matrix -- Focal Loss")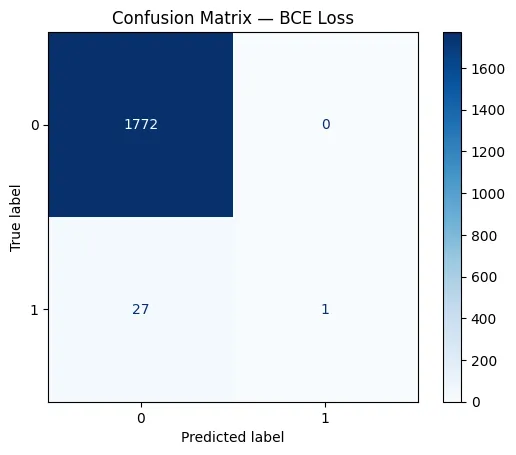

Check The complete code is here. Please feel free to check out our GitHub page for tutorials, code, and notebooks. In addition, welcome to follow us twitter And don’t forget to join our 100k+ ML SubReddit and subscribe our newsletter. wait! Are you using Telegram? Now you can also join us via telegram.

I am a Civil Engineering graduate (2022) from Jamia Millia Islamia, New Delhi and I am very interested in data science, especially neural networks and their applications in various fields.